Introduction
We often tend to think that fibrous filters behave like a sieve, where particles above a certain size are retained while smaller ones pass straight through without being captured. While this is true for some filters – such as membrane filters for liquids – air filters contradict this intuitive idea by effectively capturing both small and large particles, and showing comparatively lower efficiency only for particles of intermediate size.
High-efficiency fibrous filters account for a large proportion of the filters used worldwide. Typical applications include: respiratory protection, air sampling, cleanrooms, certain industrial processes and building ventilation systems.
A fibrous filter consists of a large number of randomly oriented fibres. These fibres form a dense “mat” that captures and holds particles throughout its entire thickness. This thickness, together with fibre diameter and mat density, are the main parameters that characterise how these filters work.
Filter performance is often expressed in terms of percentage efficiency, defined on the basis of the ratio between the downstream concentration of particles that have passed through the filter and the upstream concentration, according to the following formula:
Efficiency (%) = [1 – (Outlet concentration / Inlet concentration)] x 100
Efficiency depends on particle size and on the airflow being treated: it makes little sense to specify filter efficiency without also specifying these two parameters.
For example, NIOSH defines that a P100 respirator filter (formally equivalent in efficiency to a HEPA filter) must have a minimum efficiency of 99.97% for 0.3 micron particles at an airflow of 85 L/min. Similarly, an N95 filter must have a minimum efficiency of 95% for 0.3 micron particles at an airflow of 85 L/min.
The reason why reference is normally made to 0.3 micron particles is that particles of this size are the ones that most easily penetrate the filter. In other words, they represent the “worst-case” particle size for the filter.
Filter efficiency is lowest for these particles and higher for any other size. Below we explain why.
Filtration mechanisms
Several physical mechanisms contribute to the high capture efficiency of fibrous filters. The predominant mechanisms are interception, inertial impaction and diffusion (see Figure 1).
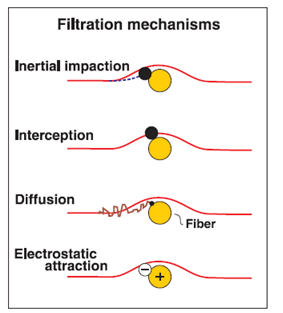
(Figure 1 – from http://blogs.cdc.gov/niosh-science-blog/2009/10/14/n95/)
Inertial impaction
Inertial impaction occurs when a particle is too large to follow the sharp changes in direction of the airflow streamlines as they move around a fibre. Because of its inertia, the particle continues along a straighter path and impacts on the fibre. This mechanism is predominant when airflow velocity is high and when the fibre mat is relatively dense.
Interception
Interception occurs when a particle carried by the gas flow passes within one particle radius of a filter fibre. The particle touches the fibre and is captured.
For a given particle size, only those streamlines that pass sufficiently close to the fibre contribute to interception. Streamlines located at distances greater than the particle radius do not contribute to this capture mechanism.
Diffusion
Before explaining the diffusion capture mechanism, it is helpful to recall some basic concepts from the kinetic theory of gases. This theory states that a gas is composed of a very large number of molecules separated by distances much greater than their own dimensions. These molecules behave like rigid spheres that travel in straight lines when they are not colliding with one another. In reality, they collide continuously, so their overall motion is a random zigzag path. This random motion is known as Brownian motion.
The diffusion capture mechanism is the result of this behaviour. Very small particles, with diameters below 0.1 micron, also tend to undergo random motion caused by collisions with gas molecules and with other particles. Diffusion is predominant at low airflow velocities and for the smallest particles. The smaller the particles and the slower the flow, the more time they have to wander randomly, increasing the probability of colliding with a fibre and being captured.
Overall filter efficiency as a function of particle size
Figure 2 shows an example of how filter efficiency varies with particle size.
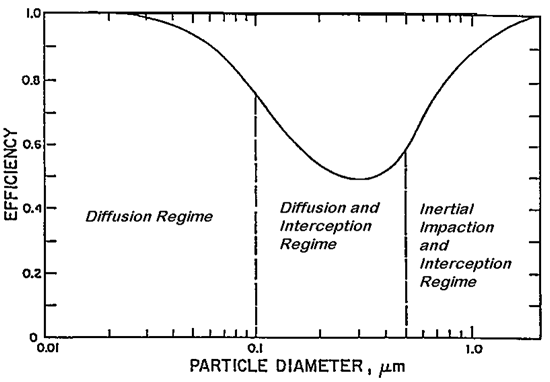
(Figure 2 – from http://blogs.cdc.gov/niosh-science-blog/2009/10/14/n95/)
As can be seen, capture efficiency is closely related to particle size.
For very small particles, with diameters below 0.1 micron, diffusion is the primary capture mechanism and the filter is very efficient.
For particles between about 0.1 and 0.4 micron in diameter, the filter is less efficient because the particles are too large for diffusion to be highly effective and still too small for interception and impaction to be fully effective.
Particles with diameters greater than about 0.4 micron fall into the range where both interception and inertial impaction become predominant, and filter efficiency increases again.
The overall result of these three capture mechanisms is a curve with the shape of an inverted bell, as illustrated in Figure 2. A fibrous filter is therefore generally least effective at removing particles between roughly 0.1 and 0.4 micron in diameter. This is why filters are tested with aerosols in this size range, in order to verify their minimum efficiency under “worst-case” operating conditions.